Representation Matters

Take a look at the table below. It shows the sample efficiency of three architectures on various tabletop tasks from the Ravens benchmark. Transporter Network (row 1) and Form2Fit (row 2) have almost identical architectures, save one component. Conv. MLP (row 3) is what naive “plug into deep neural net and regress” looks like. The differences are staggering.

So why is Transporter Network able to achieve orders of magnitude more sample efficiency than the other two baselines? The short answer is clever representation. In this short post, I’d like to expand on this and illustrate how carefully thinking about your state and action representation and the inductive biases of your neural network architecture can have a significant effect on the sample efficiency and generalization of your policy. For the interested reader, I’ve linked relevant papers at the bottom of this post.

Problem Setting

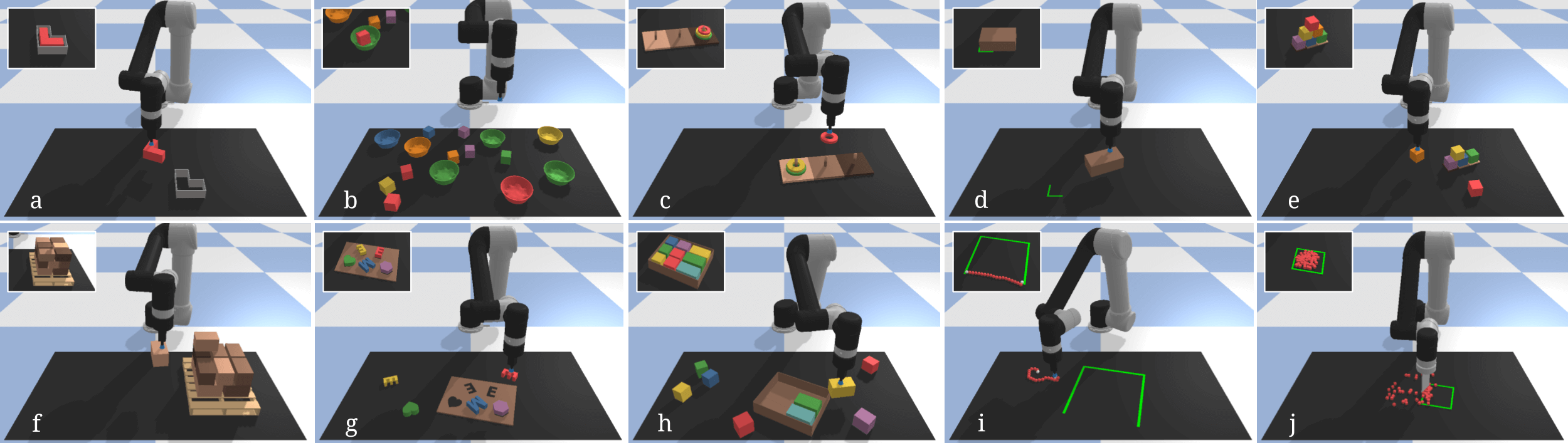
We’re interested in solving a bunch of top-down, tabletop manipulation tasks like the ones shown below. These tasks can all be completed by a sequence of two-pose motion primitives, like pick-and-place (a-i) and pushing (j).

For example, in the case of pick-and-place, the goal is to learn a mapping from visual observations to robot actions, $\pi(o_t) \rightarrow a_t = (T_{\text{pick}}, T_{\text{place}}) \in \mathcal{A},$ where $T_{\text{pick}}$ and $T_{\text{place}}$ are defined in SE(2).

Spatially-consistent Visual Representation

Most established methods for visuomotor policy learning will use raw RGB images for $o_t$, which are generated from a camera via perspective projection, and in which objects can scale or distort depending on the viewing angle and lens properties. In Transporter Network, the visual representation $o_t$ is spatially-consistent, i.e., the appearance of objects in the scene remains constant across different camera views, and each pixel $(u, v)$ represents a fixed unit of 3D space. To generate these spatially-consistent observations, RGB-D images are unprojected to a 3D pointcloud, then rendered top-down with an orthographic projection.

A spatially-consistent representation means the network doesn’t have to waste parameters to build invariances (e.g. to object distortions), so it can allocate that extra capacity to learn features that generalize better. We are thus freed from having to write complex data augmentation pipelines to train for these invariances. Instead, simpler data augmentation strategies, like applying rigid transforms to $o_t$, will simulate physically reconfiguring the scene (relative positions remaining constant) and artificially increase the size of the dataset.

Randomly (rigidly) transformed orthographic image.

Spatial Action-Value Representation

Instead of directly regressing SE(2) poses via a series of convolutional and fully-connected layers, Form2Fit and Transporter Network take a different approach: their pick and place networks output dense, pixelwise action-value maps using fully-convolutional networks (FCNs). Dense means that the output resolution is equal to the input resolution, so we get a one-to-one mapping from input to output pixels. And because the input $o_t$ is an orthographic projection of the scene, we can use camera-to-robot calibration to map each pixel $(u, v)$ in the output to a Cartesian $(x, y)$ position in the workspace. $o_t$ is also rotated $k$ times and all $k$ copies are fed in parallel to the FCN such that the convolutional layers are shared across all rotations. In doing so, we’ve discretized the entire SE(2) action space using a grid of voxels $(u, v, w)$ in $o_t$, where each pixel $(u, v)$ lies on the discretized $(x, y)$ plane, and $w$ lies on the $k$-discretized axis of rotations. This fully-convolutional action-value representation is extremely powerful for a few reasons:

1. Roto-translational equivariance. FCNs alone are translationally equivariant (by virtue of convolutions). This frees the network from having to learn redundant copies of the same filter at different positions, so if the network sees a picking pose on an object at a certain location and now the object translates, the feature maps and by extension the output picking pose translates by that same amount. Additionally, by sharing the convolutional features across the $k$ orientations, we imbue the network with rotational equivariance.

(Source) In a planar pick-and-place task, there is (i) a distribution of successful pick poses on the block, and (ii) for each pick pose, there is a corresponding distribution of successful place poses.

2. Multimodal distributions. If there’s a stochastic expert demonstrator that picks an object inconsistently (e.g., a human teleoperator picks an object on the right 50% of the time and on the left the rest of the time), or if there are multiple objects in the scene or symmetries in the object, then the picking distribution will be multi-modal in nature. Directly regressing the pick pose with an MSE loss will lead to a network output that approximates the mean of this distribution, which might not be a valid pose. This can be mitigated by having the policy parameterize a mixture of Gaussians. Instead, the fully-convolutional action-value representation elegantly deals with complex distributions since it acts like a histogram over SE(2).

3. Efficiency. In a single forward pass, FCNs can make a prediction for all possible values in this spatial representation.

In Low Dimensions, Brute Force Search

Remember at the start of this post, I mentioned that Transporter Network and Form2Fit were very similar except for 1 component. Yet Transporter is much more sample efficient. Why is this the case?

The reason is that Transporter Network is cleverly taking advantage of the action space discretization to brute force search over SE(2). In Form2Fit, a set of pick and place candidate pixels are sampled from the spatial-action maps and we take the argmin over the Cartesian product of their L2 distance (in descriptor space). 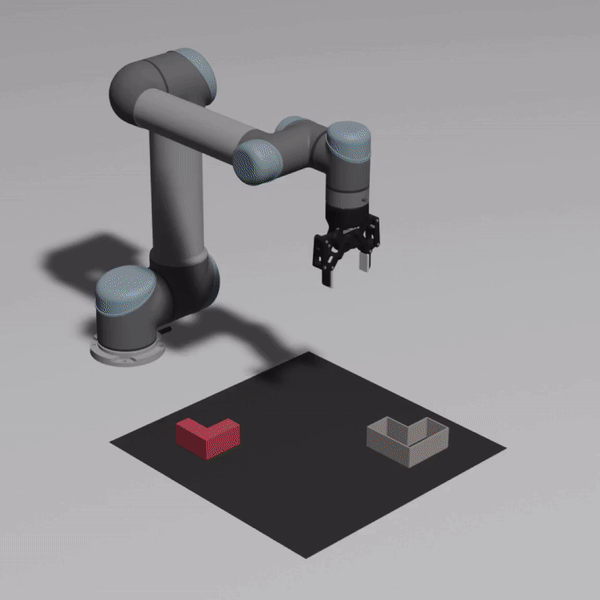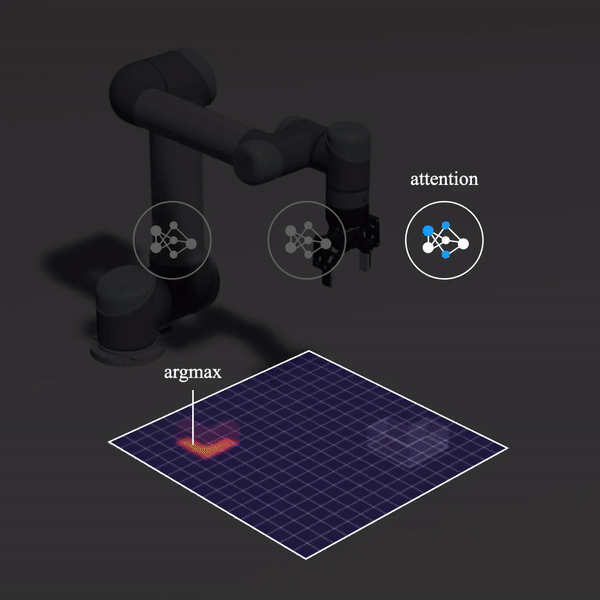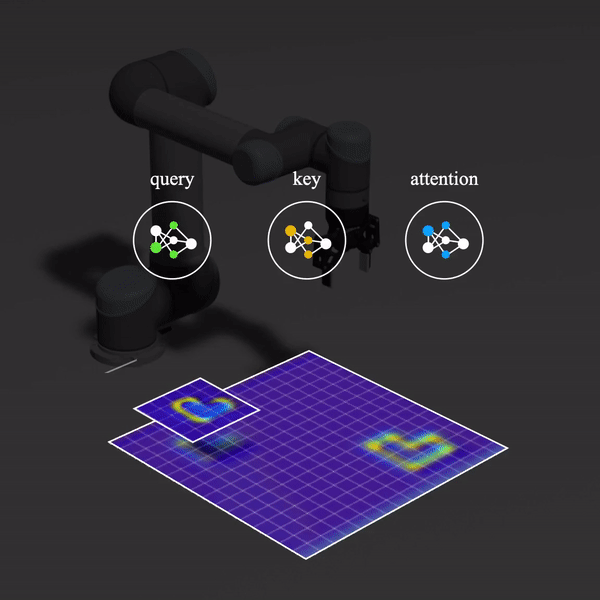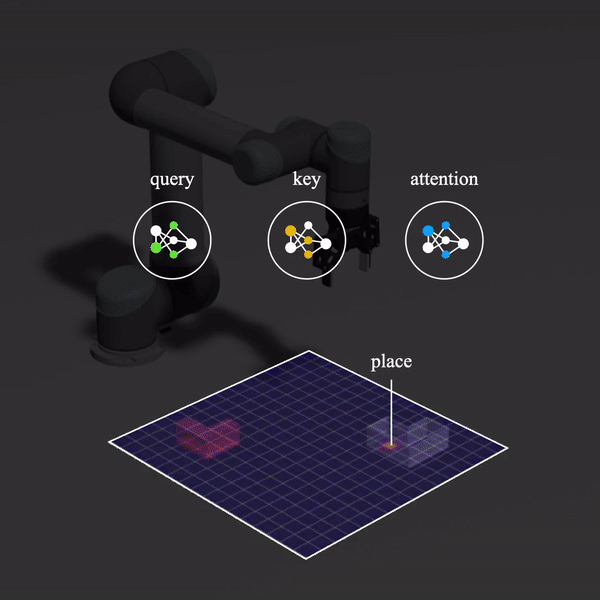Transporter Network does one better: it uses key and query networks to obtain key and query feature maps of $o_t$, then convolves a crop of the query centered at the picking location (obtained from the picking network) with the key. This operation is dubbed visuo-spatial transporting, because it takes the object in the crop and searches for the best placing position at every single point in the workspace, courtesy of the spatially-consistent representation and the pixel-aligned dense feature maps.

Another advantage of the transport operation is that the crop allows it to condition the decision on way more information than the single descriptor candidates sampled in Form2Fit (beyond what the effective receptive field of the network affords).

Closing Thoughts

Obviously, Transporter Network isn’t without its shortcomings. It’s limited to open-loop 2-pose primitives, and extending the action parameterization to SE(3) isn’t as elegant because of the curse of dimensionality. It requires precise camera-robot calibration and extra pre-processing FLOPs to convert the RGB image to an orthographic heightmap, not to mention that these heightmaps still suffer from the same occlusion and partial visibility challenges of RGB images. It’s also unclear how you would extend it to a different end-effector (e.g., a gripper) or how you would incorporate/mix different actions spaces (e.g., joint torques). But for top-down tabletop manipulation tasks, Transporter Network shines, and is a stark reminder of how clever state and action representation and their interplay with the inductive biases of neural network architectures can drastically reduce sample complexity and facilitate generalization.

References

Acknowledgments

Special thanks to Andy Zeng and Pete Florence for draft discussions.